1 – Introdução
Chama-se experimento aleatório àquele cujo resultado é imprevisível, porém pertence necessariamente a um conjunto de resultados possíveis denominado espaço amostral.
Qualquer subconjunto desse espaço amostral é denominado evento.
Se este subconjunto possuir apenas um elemento, o denominamos evento elementar.
Por exemplo, no lançamento de um dado, o nosso espaço amostral seria U = {1, 2, 3, 4, 5, 6}.
Exemplos de eventos no espaço amostral U:
A: sair número maior do que 4: A = {5, 6}
B: sair um número primo e par: B = {2}
C: sair um número ímpar: C = {1, 3, 5}
Nota: O espaço amostral é também denominado espaço de prova.
Trataremos aqui dos espaços amostrais equiprováveis, ou seja, aqueles onde os eventos elementares possuem a mesma chance de ocorrerem.
Por exemplo, no lançamento do dado acima, supõe-se que sendo o dado perfeito, as chances de sair qualquer número de 1 a 6 são iguais. Temos então um espaço equiprovável.
Em oposição aos fenômenos aleatórios, existem os fenômenos determinísticos, que são aqueles cujos resultados são previsíveis, ou seja, temos certeza dos resultados a serem obtidos.
Normalmente existem diversas possibilidades possíveis de ocorrência de um fenômeno aleatório, sendo a medida numérica da ocorrência de cada uma dessas possibilidades, denominada Probabilidade.
Consideremos uma urna que contenha 49 bolas azuis e 1 bola branca. Para uma retirada, teremos duas possibilidades: bola azul ou bola branca. Percebemos entretanto que será muito mais frequente obtermos numa retirada, uma bola azul, resultando daí, podermos afirmar que o evento "sair bola azul" tem maior probabilidade de ocorrer, do que o evento "sair bola branca".
2 – Conceito elementar de Probabilidade
Seja U um espaço amostral finito e equiprovável e A um determinado evento ou seja, um subconjunto de U. A probabilidade p(A) de ocorrência do evento A será calculada pela fórmula
p(A) = n(A) / n(U)
onde:
n(A) = número de elementos de A e n(U) = número de elementos do espaço de prova U.
Vamos utilizar a fórmula simples acima, para resolver os seguintes exercícios introdutórios:
1.1 - Considere o lançamento de um dado. Calcule a probabilidade de:
a) sair o número 3:
Temos U = {1, 2, 3, 4, 5, 6} [n(U) = 6] e A = {3} [n(A) = 1]. Portanto, a probabilidade procurada será igual a p(A) = 1/6.
b) sair um número par: agora o evento é A = {2, 4, 6} com 3 elementos; logo a probabilidade procurada será p(A) = 3/6 = 1/2.
c) sair um múltiplo de 3: agora o evento A = {3, 6} com 2 elementos; logo a probabilidade procurada será p(A) = 2/6 = 1/3.
d) sair um número menor do que 3: agora, o evento A = {1, 2} com dois elementos. Portanto,p(A) = 2/6 = 1/3.
e) sair um quadrado perfeito: agora o evento A = {1,4} com dois elementos. Portanto, p(A) = 2/6 = 1/3.
1.2 - Considere o lançamento de dois dados. Calcule a probabilidade de:
a) sair a soma 8
Observe que neste caso, o espaço amostral U é constituído pelos pares ordenados (i,j), onde i = número no dado 1 e j = número no dado 2.
É evidente que teremos 36 pares ordenados possíveis do tipo (i, j) onde i = 1, 2, 3, 4, 5, ou 6, o mesmo ocorrendo com j.
As somas iguais a 8, ocorrerão nos casos:(2,6),(3,5),(4,4),(5,3) e (6,2). Portanto, o evento "soma igual a 8" possui 5 elementos. Logo, a probabilidade procurada será igual a p(A) = 5/36.
b) sair a soma 12
Neste caso, a única possibilidade é o par (6,6). Portanto, a probabilidade procurada será igual a p(A) = 1/36.
1.3 – Uma urna possui 6 bolas azuis, 10 bolas vermelhas e 4 bolas amarelas. Tirando-se uma bola com reposição, calcule as probabilidades seguintes:
a) sair bola azul
p(A) = 6/20 = 3/10 = 0,30 = 30%
b) sair bola vermelha
p(A) = 10/20 =1/2 = 0,50 = 50%
c) sair bola amarela
p(A) = 4/20 = 1/5 = 0,20 = 20%
Vemos no exemplo acima, que as probabilidades podem ser expressas como porcentagem. Esta forma é conveniente, pois permite a estimativa do número de ocorrências para um número elevado de experimentos. Por exemplo, se o experimento acima for repetido diversas vezes, podemos afirmar que em aproximadamente 30% dos casos, sairá bola azul, 50% dos casos sairá bola vermelha e 20% dos casos sairá bola amarela. Quanto maior a quantidade de experimentos, tanto mais a distribuição do número de ocorrências se aproximará dos percentuais indicados.
3 – Propriedades
P1: A probabilidade do evento impossível é nula.Com efeito, sendo o evento impossível o conjunto vazio (Ø), teremos:
p(Ø) = n(Ø)/n(U) = 0/n(U) = 0
Por exemplo, se numa urna só existem bolas brancas, a probabilidade de se retirar uma bola verde (evento impossível, neste caso) é nula.
P2: A probabilidade do evento certo é igual a unidade.
Com efeito, p(A) = n(U)/n(U) = 1
Por exemplo, se numa urna só existem bolas vermelhas, a probabilidade de se retirar uma bola vermelha (evento certo, neste caso) é igual a 1.
P3: A probabilidade de um evento qualquer é um número real situado no intervalo real [0, 1].
Esta propriedade, decorre das propriedades 1 e 2 acima.
P4: A soma das probabilidades de um evento e do seu evento complementar é igual a unidade.Seja o evento A e o seu complementar A'. Sabemos que A U A' = U.
n(A U A') = n(U) e, portanto, n(A) + n(A') = n(U).
Dividindo ambos os membros por n(U), vem:
n(A)/n(U) + n(A')/n(U) = n(U)/n(U), de onde conclui-se:
p(A) + p(A') = 1
Nota: esta propriedade simples, é muito importante pois facilita a solução de muitos problemas aparentemente complicados. Em muitos casos, é mais fácil calcular a probabilidade do evento complementar e, pela propriedade acima, fica fácil determinar a probabilidade do evento.
P5: Sendo A e B dois eventos, podemos escrever:
p(A U B) = p(A) + p(B) – p(A Ç B)Observe que se A ÇB= Ø (ou seja, a interseção entre os conjuntos A e B é o conjunto vazio), então p(A U B) = p(A) + p(B).
Com efeito, já sabemos da
Teoria dos Conjuntos que
n(A U B) = n(A) + n(B) – n(A
ÇB)
Dividindo ambos os membros por n(U) e aplicando a definição de probabilidade, concluímos rapidamente a veracidade da fórmula acima.
Exemplo:
Em uma certa comunidade existem dois jornais J e P. Sabe-se que 5000 pessoas são assinantes do jornal J, 4000 são assinantes de P, 1200 são assinantes de ambos e 800 não lêem jornal. Qual a probabilidade de que uma pessoa escolhida ao acaso seja assinante de ambos os jornais?
SOLUÇÃO:
Precisamos calcular o número de pessoas do conjunto universo, ou seja, nosso espaço amostral. Teremos:
n(U) = N(J U P) + N.º de pessoas que não lêem jornais.
n(U) = n(J) + N(P) – N(J ÇP) + 800
n(U) = 5000 + 4000 – 1200 + 800
n(U) = 8600
Portanto, a probabilidade procurada será igual a:
p = 1200/8600 = 12/86 = 6/43.
Logo, p = 6/43 = 0,1395 = 13,95%.
A interpretação do resultado é a seguinte: escolhendo-se ao acaso uma pessoa da comunidade, a probabilidade de que ela seja assinante de ambos os jornais é de aproximadamente 14%.(contra 86% de probabilidade de não ser).








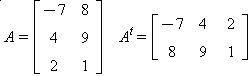
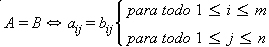
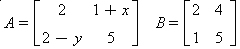
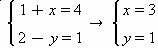
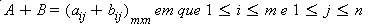
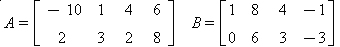
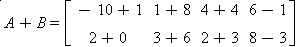
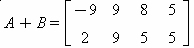
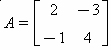
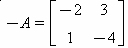
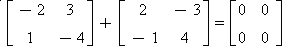
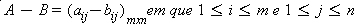
 , calcule 3a31 – 5a42.
, calcule 3a31 – 5a42.
 e
e  e
e  e
e  sejam iguais.
sejam iguais. é oposta à matriz
é oposta à matriz  .
.