EQUAÇÃO DO 2º GRAU COMPLETA

Equações do tipo ax + b = 0, com a e b números reais e a ≠ 0, são consideradas do 1º grau e possuem uma única raiz real. Já as equações completas do 2º grau possuem a seguinte lei de formação ax² + bx + c = 0, com a, b e c números reais e a ≠ 0 e devem ser resolvidas com o uso da fórmula de Bháskara:



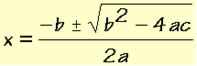
onde a, b e c são os coeficientes da equação.

Discriminante: ∆ = b² - 4ac
Condições:
∆> 0 (número positivo): duas raízes reais e diferentes
∆< 0 (número negativo): nenhuma raiz real
∆= 0: duas raízes reais

Exemplo 1
Quais os coeficientes da equação 2x² + 5x – 6 = 0?
a = 2 b = 5 c = – 6

Exemplo 2 
Calcule as raízes, se existirem, da seguinte equação do 2º grau: x² + 4x – 5 = 0.
Temos que: a = 1 b = 4 c = -5



Nem sempre o valor do discriminante será um número quadrado perfeito, acompanhe o exemplo 3:
x² - 3x + 1 = 0


EXERCÍCIOS
Resolva as equções abaixo:

1) 8x² -12x +4 = 0

2) -12x² + 4x +16 = 0

3) x² -5x +4 = 0

4) 3x² + 7x +2 = 0

5) -x² -11x -10 = 0

6) 3x² -2x -1 = 0

7) -2x² -3x +2 = 0

8) -2x² -7x -5 = 0

9) -2x² -x +6 = 0

10) -x² + 9x -8 = 0

ESTUDANDO PRODUTOS NOTÁVEIS

Há certos produtos que ocorrem freqüentemente no calculo algébrico e que são chamados produtos notáveis. Vamos apresentar aqueles cujo emprego é mais freqüente.

QUADRADO DA SOMA DE DOIS TERMOS

Observe: (a + b)² = ( a + b) . (a + b)
_______________= a² + ab+ ab + b²
_______________= a² + 2ab + b²

Conclusão:
(primeiro termo)² + 2.(primeiro termo) . (segundo termo) + (segundo termo)²

Exemplos :

1) (5 + x)² = 5² + 2.5.x + x² = 25 + 10x + x²

2) (2x + 3y)² = (2x)² + 2.(2x).(3y) + (3y)² = 4x² + 12xy + 9y²

Exercícios

1) Calcule

a) (3 + x)² = 
b) (x + 5)² = 
c) ( x + y)² = 
d) (x + 2)² = 
e) ( 3x + 2)² = 
f) (2x + 1)² = 
g) ( 5+ 3x)² = 
h) (2x + y)² = 
i) (r + 4s)² = 
j) ( 10x + y)² = 
l) (3y + 3x)² =
m) (-5 + n)² = 
n) (-3x + 5)² =
o) (a + ab)² = 
p) (2x + xy)² = 
q) (a² + 1)² =
r) (y³ + 3)² =
s) (a² + b²)² =
t) ( x + 2y³)² =
u) ( x + ½)² = 
v) ( 2x + ½)² =
x) ( x/2 +y/2)² = 

QUADRADO DA DIFERENÇA DE DOIS TERMOS

Observe: (a - b)² = ( a - b) . (a - b)
______________= a² - ab- ab + b²
______________= a² - 2ab + b²

Conclusão:
(primeiro termo)² - 2.(primeiro termo) . (segundo termo) + (segundo termo)²

1) ( 3 – X)² = 3² + 2.3.X + X² = 9– 6x + x²

2) (2x -3y)² = (2x)² -2.(2x).(3y) + (3y)² = 4x² - 12xy+ 9y²

Exercícios

1) Calcule

a) ( 5 – x)² = 
b) (y – 3)² = 
c) (x – y)² = 
d) ( x – 7)² =
e) (2x – 5) ² =
f) (6y – 4)² = 
g) (3x – 2y)² = 
h) (2x – b)² =
i) (5x² - 1)² = 
j) (x² - 1)² =                   
l) (9x² - 1)² =
m) (x³ - 2)² =
n) (2m⁵ - 3)² = 
o) (x – 5y³)² =
p) (1 - mx)² =
q) (2 - x⁵)² =
r) (-3x – 5)² =
s) (x³ - m³)² =

PRODUTO DA SOMA PELA DIFERENÇA DE DOIS TERMOS

(a + b). (a – b) = a² - ab + ab - b² = a²- b²

conclusão:
(primeiro termo)² - (segundo termo)²

Exemplos :

1) ( x + 5 ) . (x – 5) = x² - 5² = x² - 25
2) (3x + 7y) . (3x – 7y) = (3x)² - (7y)² = 9x² - 49y²

EXERCÍCIOS

1) Calcule o produto da soma pela diferença de dois termos:

a) (x + y) . ( x - y) = 
b) (y – 7 ) . (y + 7) =
c) (x + 3) . (x – 3) = 
d) (2x + 5 ) . (2x – 5) =
e) (3x – 2 ) . ( 3x + 2) = 
f) (5x + 4 ) . (5x – 4) =
g) (3x + y ) (3x – y) =
h) ( 1 – 5x) . (1 + 5x) =
i) (2x + 3y) . (2x – 3y) =
j) (7 – 6x) . ( 7 + 6x) =
l) (1 + 7x²) . ( 1 – 7x²) = 
m) (3x² - 4 ) ( 3x² + 4) = 
n) (3x² - y²) . ( 3x² + y²) =
o) (x + 1/2 ) . ( x – 1/2 ) =
p)(x – 2/3) . ( x + 2/3) =
q)( x/4 + 2/3) . ( x/4 – 2/3) =

CONVERSÃO DE MEDIDAS DE ÂNGULOS

Quando medimos o ângulo de um arco utilizamos como unidade o grau ou o radiano. Temos que 1º (um grau) possui 60’ (sessenta minutos) e 1’ (um minuto) possui 60” (sessenta segundos). Uma circunferência possui 360 arcos de abertura igual a 1º. No caso da medida em radianos, dizemos que o arco mede um radiano (1 rad) se o seu comprimento for igual ao comprimento do raio da circunferência que se encontra o arco medido.

Α tabela a seguir mostra algumas relações entre as unidades em graus e radianos.

Convertendo Graus em Radianos

Na conversão de graus para radianos utilizamos uma regra de três simples, por exemplo:

20º em radianos

graus	radianos
20º	x
180º	π rad

15º em radianos

graus	radianos
15º	x
180º	π rad

120º em radianos

graus	radiano
120º	x
180º	π rad

150º em radianos

graus	radiano
150º	x
180º	π rad

300º em radianos

graus	radiano
300º	x
180º	π rad

Convertendo Radianos em Graus

Na conversão de radianos para graus, basta substituirmos o valor de π por 180º. Veja exemplos:

OPERAÇÕES COM NÚMEROS INTEIROS (Z)

Qualquer adição, subtração ou multiplicação de dois números inteiros sempre resulta também um número inteiro. Dizemos então que estas três operações estão bem definidas em Z ou, equivalentemente, que o conjunto Z é fechado para qualquer uma destas três operações.
As divisões, as potenciações e as radiciações entre dois números inteiros nem sempre têm resultado inteiro. Assim, dizemos que estas três operações não estão bem definidas no conjunto Z ou, equivalentemente, que Z não é fechado para qualquer uma destas três operações.

Adições e subtrações com números inteiros
Existe um processo que simplifica o cálculo de adições e subtrações com números inteiros. Observe os exemplos seguintes:

Exemplo1: 
Calcular o valor da seguinte expressão:
10 - 7 - 9 + 15 - 3 + 4

Solução:Faremos duas somas separadas

• uma só com os números positivos: 10 + 15 + 4 = +29
• outra só com os números negativos: (-7) + (-9) + (-3) = -19

Agora calcularemos a diferença entre os dois totais encontrados: +29 - 19 =  +10

Atenção: É preciso dar sermpre ao resultado o sinal do número que tiver o maior valor absoluto!

Multiplicação e divisões com números inteiros
Nas multiplicações e divisões de dois números inteiros é preciso observar os sinais dos dois termos da operação:

Exemplos:

Sinais iguais (+)	Sinais opostos (-)
(+) × (+) = +	(+) × (-) = -
(-) × (-) = +	(-) × (+) = -
(+) ÷ (+) = +	(+) ÷ (-) = -
(-) ÷ (-) = +	(-) ÷ (+) = -

1-     Calcule o valor das expressões numéricas:

a)      45 – { 4 . [( 9 . 12 – 14 . 7 ) : ( 15 – 5 . 2 )]}=

b)      20 : 4 + 3 . 2 – 15 : 3=

c)      [ 25 – ( 18 : 3 )]. { 5 – [ 18 – ( 4 . 5 – 4 )]}=

d)      { 38 + [( 143 : 11 + 7 ) – 5 . 2]}: 6  =

e)      2 . [ ( 5 – 2 ) . ( 3 + 2 . 7 )] – 2 =

 

 

f)  ( 8 + 6 . 8 : 4) + [ 3 + 15 : 5 + 5]    =    

  

 

g) 25 : 5 + ( 8 + 3 . 10 : 2) + ( 4 . 3 – 14 : 7)=

 

 

h) {[ 12 – 5 x 2 + ( 24 : 3 – 7) ] + 5} =     

     

 

 i) ( 32 – 8 : 4) + ( 45 : 9 + 8) – 6 =

EXPRESSÕES NUMÉRICAS COM AS QUATRO OPERAÇÕES

Nessas expressões, as operações se realizam obedecendo à seguinte ordem:

1º) multiplicações e divisões

2º) adições e subtrações

Se houver sinais de associação (parênteses, colchetes e chaves) devemos proceder da seguinte maneira:

1º) As contas dentro dos parênteses seguindo a ordem acima colocada

2º) As contas dentro dos colchetes seguindo a ordem acima colocada

3º) As contas dentro das chaves seguindo a ordem acima colocada


EXEMPLOS

1º) 15+[(3x6-2)-(10-6:2)+1]=
      = 15+[(18-2)-(10-3)+1]=
      =15+[16-7+1]=
      =15+[9+1]=
      =15+10=
      =25

2º) 50-{40-3x[5-(10-7)]}=
      = 50-{40-3x[5-3]}=
      = 50-{40-3x2}=
      = 50-{40-6}=
      = 50-34=
      =16

EXERCÍCIOS

1) Calcule as expressões

a) 3x75+3x25 = 

b) 5x97+5x3 = 

c) 4x101+4x99 = 

d) 20x47+80x47 = 

e) 12+16:8x3-5 = 

f) 100-6x7+8:2 = 

g) 64:8+5x5-3 = 

h) 1+3+5x7-9:3 = 

2) Calcule o valor das expressões:

a) 7+15:3 = 

b) 4x5+1 = 

c) 10:2+8 = 

d) 32+12:2 = 

e) 20:10+10 = 

f)7x3-2x5 = 

g)40-2x4+5 = 

h)4x3+10:2 = 

i)50-16:8+7 = 

j)32:4:2:2 =

3) Calcule o valor das expressões

a) (13+2)x3+5 = 

b)(7+2)x(3-1) = 

c)(4+2x5)-3 = 

d) 20-(15+6:3) = 

e)15+[6+(8-4:2)] = 

f)40-[3+(10-2):2] = 

g)[30+2x(5-3)]x2-10 = 

h) 10+[4+(7x3+1)]-3 = 

4) Calcule o valor das expressões

a) (3+2)x(5-1)+4 = 

b) 82-8x7:(4-1x3) = 

c) 25-[10-(2x3+1)] = 

d) 70-[12+(5x2-1)+6] = 

e)8:2+[15-(4x2+1)] = 

f)9+[4+2x(6-4)+(2+5)]-8 = 

g) 50+{10-2x[(6+4:2)-(10-3)]} = 

h)180:{10+2x[20-45:(13-2x5)]} = 


5) Calcule o valor das expressões:

a) 70:7-1= 

b) 20+3x2= 

c) 30+10:10 = 

d) 150-7x12= 

e) 48:16+20:4 = 

f) 10-8:2+3 = 

g) 30:5-1+2x3 = 


6) Calcule as expressões:

a) (3+4)x(9-8) = 

b) (20+8):(3+4) = 

c) 15+8x(2+3) = 

d) (5+3x2)-1= 

e) 25+(8:2+1)-1= 

f) 15+[5x(8-6:2)] = 

g) 50-[13-(10-2):2] = 

h) [40+2x(7-5)]x2-20 = 

7) Calcule o valor das expressões:

a) 16+[10-(18:3+2)+5] = 

b) 25-[12-(3x2+1)] = 

c) 90-[25+(5x2-1)+3] = 

d) 45+[(8x5-10:2)+(18:6-2)] =

e) 50-2x{7+8:2-[9-3x(5-4)]} = 

f) 100-3x{5+8:2-[3x(7-6)]} = 

8) Determine o valor de cada expressão

a) 1000 - [(2 . 4 - 6) + ( 2 + 6 . 4)] = 

b) 60 + 2 . {[ 4 . ( 6 + 2 ) - 10 ] + 12} = 

c) [( 4 + 16 . 2) . 5 - 10] . 100 = 

d) { 10 + [ 5 . ( 4 + 2 . 5) - 8] . 2 } - 100 = 

e) 80 - 5 . ( 28 - 6 . 4 ) + 6 - 3 . 4 = 

9) Calcule

a) 4 . ( 10 + 20 + 15 + 30) = 

b) (10 . 6 + 12 . 4 + 5 . 8 ) - 40 = 

c) [ 6 . ( 3 . 4 - 2 . 5) - 4 ] + 3 . ( 4 - 2) - ( 10 : 2 ) = 

d) 67 + { 50 . [ 70 : ( 27 + 8 ) + 18 : 2 ] + 21 } = 

e) [ 30 . ( 9 - 6)] + { 30 : ( 9 + 6 ) ] = 

f) 58 - [ 20 - ( 3 . 4 - 2) : 5 ] = 

g) 40 + 2 . [ 20 - ( 6 + 4 . 7 ) : 2 ] = 


10) Calcule o valor das expressões

a) (12 + 2 . 5) - 8 = 

b) 25 - ( 15 + 6 : 3) = 

c) 25 +[7 + ( 8 - 4 :2)] = 

d) 60 - [8 + ( 10 - 2 ) : 2] = 

e) 80 - [ 22 + ( 5 . 2 - 1 ) + 6] = 

f) 14 : 2 + [ 13 - ( 4 . 2 + 1 ) ] = 

g) [ 30 + 2 x ( 5 – 3 ) ] x 2 – 10 =

h) 20 : 10 + 10 =

i) 10 + [ 4 + ( 7 x 3 + 1 ) ] – 3 =


11) Resolva as expressões numéricas:

a) 8 – ( 1 + 3) =

b) 7x 3 – 2 x 5 = 

c) ( 13 – 7 ) + 8 – 1 = 

d)4 x 3 + 10 : 2 = 

e) 15 – ( 3 + 2 ) – 6 = 

f) 40 – 2 x 4 + 5 = 

g) ( 10 – 4 ) – ( 9 – 8 ) + 3 = 

h) 50 – 16 : 8 + 7 = 

i) 50 – [37 – ( 15 – 8 ) ] = 

j) 32 : 4 : 2 : 2 = 

l) 28 + [ 50 – ( 24 – 2 ) – 10 ] = 

m) ( 13 + 2) x 3 + 5 = 

n) 20 + [ 13 + ( 10 – 6 ) + 4 ] = 

o) ( 7 + 2 ) x ( 3 – 1 ) = 

p) 52 – { 12 + [ 15 – ( 8 – 4 )]} =

q) ( 4 + 2 x 5 ) – 3 =

r) 7 + 15 : 3 =

s) 20 – ( 15 + 6 : 3) =

t) 4 x 5 + 1 =

u) 15 + [ 6 + ( 8 – 4 : 2 )] =

v) 10 : 2 + 8 =

x) 40 – [ 3 – (10 – 2 ) : 2 ] =

z) 32 + 12 : 2 =

ATIVIDADES - RAZÕES TRIGONOMÉTRICAS

a) No triângulo retângulo da figura abaixo, determine as medidas de x e y indicadas (Use: sen 65° = 0,91; cos 65° = 0,42 ; tg 65° = 2,14)

b) Considerando o triângulo retângulo ABC da figura, determine as medidas a e b indicadas. (Sen 60° = 0,866)

c) Sabe-se que, em um triângulo retângulo isósceles, cada lado congruente mede 30 cm. Determine a medida da hipotenusa desse triângulo.

Nos triângulos das figuras abaixo, calcule tg Â, tg Ê, tg Ô:

d)                            
e)      
f) 

g) Sabendo que o triângulo retângulo da figura abaixo é isósceles, quais são os valores de tg  e tg Ê?

h) Encontre a medida RA sabendo que tg  = 3.

Calcule corretamente os valores de x e y nos triângulos abaixo:

i)        
j) 

EXERCÍCIOS SOBRE EXPRESSÕES ALGÉBRICAS E MONÔMIOS

1)Calcule o valor numérico das expressões algébricas:

a)3m – 2n, para m=11 e n=–12
b)x² – 6x, para x = – 5
c)x²  – 9x + 14, para x = 2
d)(a – 2)(a – 1)(a – 4), para     a = – 1

e)b² – 4ac, para a = 1, b = 2 e             c = – 15.

f)m² – 2mn + n², quando m = –1 e      n = ¼.
g)3(x² – y²) – 10(x + y)(x – y), quando  x = – 2 e y = 2.

2)     Efetue as operações indicadas:

a)(2x³ – 3x² + x – 1) + (5x³ + 6x² – 7x + 3)
b)(– 8y² – 12y + 5) + (7y² – 8)
c)(2ax³ – 5a²x – 4by) + (5ax³ + 7a²x + 6by)
d)(a² – b²) + (a² – 3b² – c) + (5c – 2b² – a²)
e)(3y² – 2y – 6) – (7y² + 8y + 5)
f)(8x³ – 4x² + 3x – 5) – (6x³ – 7x² + 5x – 9)
g)(2x³ – 3x + 1) – (– 4x² + 3)
h)(2x³ – 5x² + 8x – 1) – (– 3x³ + 5x² – 5x + 6)
i)(x² – 5xy + y²) + (3x² – 7xy + 3y²) – (4y² – x²)

3)Calcule os produtos entre os monômios:

a)(2x) . (3x²)
b)(–3y) . (4y²)
c)(5a) . (–3b)
d)(–4x²y) . (–3xy²)
e)(–5ab). (3a)
f)(–a²b).(ab³c)
g)(–m) . (–3m²) . (2m³)
h)(–4a).( –3b). (2ab)

4)Calcule os quocientes entre monômios:

a)(–12a) : (–3a)
b)(–20a⁵) : (4a²)
c)(36xy³) : (4y)
d)(18xy³) : (–2x)
e)(–14xy³) : (–-7xy²)
f)(–24a³b²) : (4ab⁵)
g)(–2ab) : (3b)
h)(5x³y) : (–-7x⁴y)

5)Calcule as potências:

a)(–3x)²
b)(–3x²)²
c)(–3x)⁰
d)(6x²y)²
e)(–2a³b²)³
f)(4a³)³

DIVIRTA-SE !!!!!!